컴퓨터 공학에 입문한 뒤 대부분 처음으로 배우는 소수 판별 알고리즘은 에라토스테네스의 체 알고리즘이다.
에라토스테네스의 체는 소수를 판별하고 싶은 범위 안의 소수인 수의 모든 배수를 차례로 제거해서 원하는 수의 범위에서 어떤 수가 소수인지 판별 할 수 있는 알고리즘이다.
이는 꽤나 직관적인 알고리즘으로, 알고리즘이 작동하는 방식을 보면 소수라는 체로 소수가 아닌 수를 거르는 것처럼 보인다.
따라서 알고리즘의 고안자인 에라토스테네스의 이름과 체를 붙여서 에라토스테네스의 체 라는 이름을 가지고 있다.
에라토스테네스의 체는 O(N^2) 시간복잡도를 가진 알고리즘이다.
그런데 놀랍게도 에라토스테네스의 체를 가르쳐 준 후, 컴퓨터 공학 학부를 졸업할 때까지 일반적인 학부 과정상에서 소수 판별에 대한 더 효율적인 알고리즘에 대한 언급은 하지 않는다.
그 이유는 O(N^2)보다 효율적인 소수 판별 알고리즘을 이해하기 위해서는 갑자기 난이도가 미친듯이 확 뛰기 때문이다.
이 글에서는 에라토스테네스의 체보다 빠른 소수 판별 알고리즘인 밀러 - 라빈 소수 판별법을 설명해보도록 하겠다.
밀러 - 라빈 소수 판별법으로 이름 붙여진 이 소수 판별 알고리즘은 일단 (고속 푸리에 변환을 사용한다면)O(Nlog^2N)또는 O(Nlog^3N)시간 안에 어떤 수가 소수인지 확률적으로 판단할 수 있다.
확률적이라는게 어떤 말일까? 이 말은 "이 정리를 만족하면 아마도 소수일 것같다.(probable prime)"라는 말과 같다.
소수면 소수고 아니면 아닌거지 저게 대체 무슨 소리일까?
저렇게 표현하는 이유는 소수가 아닌 수 중 위 정리를 만족할 수 있는 수가 발견됐기 때문이다.
"엥 그러면 정확한 소수를 구해야할 때 쓰면 안되는 알고리즘 아닌가??!!" 라고 생각 할 수 있지만 일단 long long의 자료형 범위정도의 크기는 수학에서는 작은 수라고 표현할 정도로 작은 범위이기 때문에, long long 범위에서는 정확히 소수라고 판별할 수 있다.
이 알고리즘을 이해하기 위해서는 정수론에 대한 정리 2가지를 알아야 한다.
이 글에서는 정수론 내용 중 알고리즘을 이해하는대에 필요한 부분만 뽑아서 설명해서 정수론 내용을 모르더라도 알고리즘을 이해할 수 있도록 설명해보도록 하겠다.
우선 정수론에 대한 정리를 설명하기에 앞서 정수론의 기호에 대한 설명은 다음과 같다.

위의 표현 방식을 이해하고 글을 읽어주시길 바란다.
[보조 정리 1] 페르마의 소정리(Fermat's Little Theorem)

위의 정리는 어떤 소수 p와 아무 정수 a를 알 때, a를 p로 나눈 나머지가 0이 아니라면
1. a를 p번 곱한 수를 소수 p로 나눈 나머지 = a를 소수 p로 나눈 나머지
2. a를 p-1번 곱한 수를 소수 p로 나눈 나머지 = 1
위의 1, 2번이 성립한다는 정리이다.
[보조 정리 2]

X^2 - 1이 p의 배수이므로, X-1 또는 X+1이 p의 배수가 된다. 따라서 위의 보조 정리가 성립한다.
이제 밀러 - 라빈 소수 판별법을 이해하는데 필요한 정수론적 기초를 알게 됐다.
지금부터는 밀러 - 라빈 소수 판별법에 대해서 설명해보도록 하겠다.
먼저 N이 2가 아닌 소수라고 가정하자. 그러면 N-1은 짝수가 되고(2를 제외한 모든 소수는 짝수가 아니다. 2의 배수가 되기 때문),
N-1을 홀수가 될 때까지 2로 나눠주면 다음과 같이 표현이 가능하다. (d는 더이상 2로 나눠지지 않는 홀수이다.)

N이 소수이기 때문에 양의 정수 a에 대해서 페르마의 소정리를 만족하게 된다. 따라서 다음 식을 만족한다.

따라서 [보조 정리 2]에 의해서 다음 식을 만족한다.

만약 두 번째 식과 같은 경우에는 또 다시 [보조 정리 2]를 이용할 수 있다.
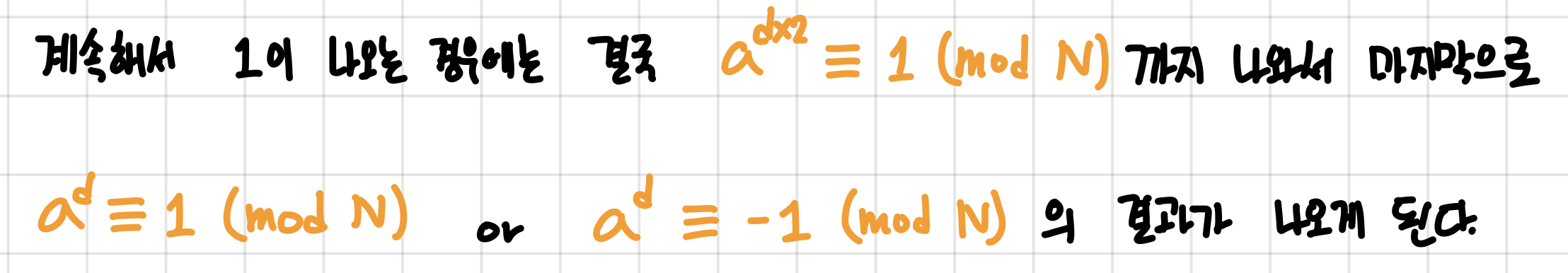
여기서는 d가 홀수이기 때문에 더 이상 [보조 정리 2]를 사용할 수 없다.
위 과정을 통해서 N이 소수라면 N보다 작은 양의 정수 a에 대해서 다음 줄 중 하나를 만족한다고 할 수 있다.
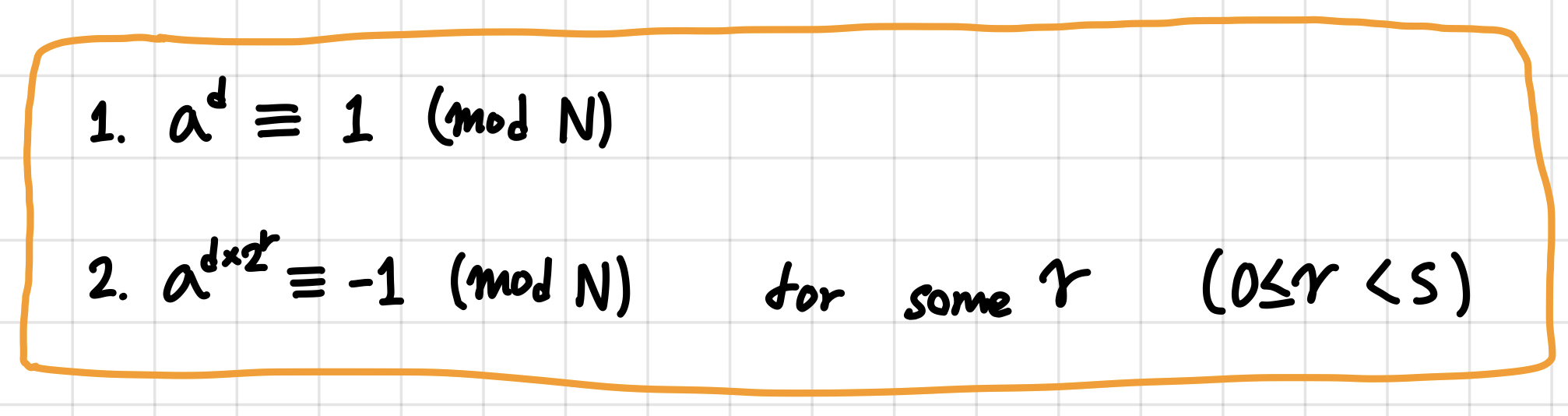
위의 결과를 이용해서 어떤 수 N이 소수인지 아닌지 빠르게 판별 가능하다.
여기서 "왜 저 결과를 만족하면 N이 소수인가?" 라는 의문이 생긴다면 위 결과는 우리가 밀러 - 라빈 소수 판별법을 설명할 때 가장 처음에 N이 2가 아닌 소수라고 가정하고 나온 결과라는 것을 떠올려보길 바란다.
이렇게 잘 구해놓은 공식을 컴퓨터 공학에서 사용하기 위해서 알아야할 것이 있는데, int와 long long 범위에 해당하는 수 N의 소수 판별을 하기 위해서는
다음과 같은 a들에 대한 위 테스트가 통과하면 소수라고 결정론적으로 말할 수 있다는 것이 밝혀져있다.
int 범위 : a = 2, 7, 61
long long 범위 : a = 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31 (2~31까지의 소수)
따라서 일반적으로 우리가 이용하게 될 알고리즘에서는 수의 범위에 따라 저 a들에 대한 테스트만 진행해보고 모든 테스트를 통과하는지 확인하면 된다.
다음에는 고속 푸리에 변환에 대한 설명으로 찾아도록 하겠다... 너무 어렵긴 한데 설명하면서 이해해보려 한다.
'CS(Computer Science) > 알고리즘' 카테고리의 다른 글
| 삼성SDS 2023 동계(상반기) 대학생 알고리즘 특강 후기 (14) | 2023.01.25 |
|---|